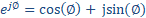Carrier mixer amplitude limit
Hi,
I want to use the carrier_mixer_us in ocpi.comp.sdr.dsp component to down convert a signal.
Ideally I would want the input wave to have the same amplitude as the output wave however this does not seem to be possible due to the carrier_amplitude property having a maximum allowed value of 14,060.
Since the property is scaled by 1.646760258, this brings the amplitude of the mixer wave to 23170.475 or roughly sqrt(2) * 2^15. I would understand if the amplitude was limited to 2^15 to prevent overflow but what is the reason for this sqrt(2) factor?
Before outputting, the result of each multiplication is shifted right by 15 (both I and Q) i.e scaled by 1 / 2^15. Therefore with the maximum mixer amplitude, the resulting wave’s amplitude will be roughly 1/sqrt(2) that of the input wave.
It is also quite counterintuitive that the input amplitude of the carrier wave is being scaled this way. Would it not be possible to provide the true amplitude to the carrier_amplitude property and have the worker do the necessary scaling? If not, renaming the property to indicate that it is not the actual amplitude would be useful.
Thanks,
Dan
Hi,
Apologies for the delayed response to this.
I asked this question to several people who were / are involved with the
creation and maintenance of this worker / component.
These are their responses, which I have slightly edited to fix formatting
and remove names, etc.
I hope the formatting is retained or this might be quite hard to read :D
--- First Response ---
This is explained in the documentation:
However, the term carrier_amplitude may be misleading, carrier_gain would
be better.
In (9) we are looking to define the gain A for some given complex sample -
the gain is relative to the input so we consider the input on a unit
circle, i.e. x and y are in the range -1 to 1.
Substituting in (9) for the point where the term multiplying A is maximal
(x = x_max and y = -x_max):
A ( x_max * cos (theta) – (-x_max) * sin( theta) )
----------------------------------------------------------------- < x_max
2^15
As x_max is 1 and the largest value of cos(theta) + sin(theta) is sqrt(2)
we then get:
A * sqrt(2)
-------------- < 1
2^15
Solving for A:
A * sqrt(2)
-------------- = 1
2^15
A * sqrt(2) = 1 * 2^15 = 2^15
A = 2^15 / sqrt(2) = 23170.475….
A is scaled by 1.64…. and so carrier_amplitude should be set to 14070 for a
gain of 1 through the component.
However, the underlying cordic can over/under-shoot so we recommend using
the value 14,060.
There is (in my opinion) an unnecessary limitation in the C++
implementation which sets an upper bound of the carrier_amplitude value to
14,060 – it is perfectly reasonable to use this component as a gain block –
i.e. setting the value to 28,000 would double the output amplitude relative
to the input.
(if you consider the input to be half scale (x = 0.5, y = 0.5, x_max = 1)
and substitute in (9) you get 28,140).
I did test the RCC implementation and the above holds, I believe the RCC
and HDL implementations are both tested against the same Python based model
– so have no reason to expect the HDL version is any different.
*--- *Second Response ---
I have been doing some thinking on this also and I think I see what Dan is
getting at…but also understand why it is designed as is.
The issue Dan is bringing up is specifically with this bit -> “A is maximal
(x = x_max and y = -x_max)”. If the carrier mixer input is a “perfect” iq
tone, as it is in Dan case, with sin and cos waveforms 90 degrees apart the
condition “x = x_max and y = -x_max” never occurs (see below that there is
never a point in time where x is 1 and y is 1 (or -1)).
[image: cid:image003.png@01DA5377.D1D769A0]
Euler’s formula is the easiest way to understand this (I reckon…):
When frequency shifting, Dan wants to realise the below formula, where is
the input signal and is the generated signal.
However, what is currently done is an acknowledgment that the input
waveform might not be a “perfect” since wave and therefore is accounting
for the “x = x_max and y = -x_max)” condition occurring.
So the term is reduced to , since the magnitude of gives 1, which ensures
whatever the input is there is no overflow. To be clear, the is and (the
amplitude of the generated waveform).
In summary, I think how we have it implemented now is correct since it
ensures a messy input waveform never overflows on the output when it is
mixed. But a good compromise to allow for Dan’s “perfect” input waveform
use case is as the first reply says: adding the ability to set the
carrier_amplitude to a value such that an amplitude of 32767 instead of
23170 is achieved for the generated waveform.
I will relay this information onto the ocpi.comp.sdr developers to add to
their backlog.
I hope this was helpful.
Kind Regards,
Dom Walters
On Wed, Jan 24, 2024 at 4:22 PM dwp@md1tech.co.uk wrote:
Hi,
I want to use the carrier_mixer_us in ocpi.comp.sdr.dsp component to down
convert a signal.
Ideally I would want the input wave to have the same amplitude as the
output wave however this does not seem to be possible due to the
carrier_amplitude property having a maximum allowed value of 14,060.
Since the property is scaled by 1.646760258, this brings the amplitude of
the mixer wave to 23170.475 or roughly sqrt(2) * 2^15. I would understand
if the amplitude was limited to 2^15 to prevent overflow but what is the
reason for this sqrt(2) factor?
Before outputting, the result of each multiplication is shifted right by
15 (both I and Q) i.e scaled by 1 / 2^15. Therefore with the maximum mixer
amplitude, the resulting wave’s amplitude will be roughly 1/sqrt(2) that of
the input wave.
It is also quite counterintuitive that the input amplitude of the carrier
wave is being scaled this way. Would it not be possible to provide the true
amplitude to the carrier_amplitude property and have the worker do the
necessary scaling? If not, renaming the property to indicate that it is not
the actual amplitude would be useful.
Thanks,
Dan
discuss mailing list -- discuss@lists.opencpi.org
To unsubscribe send an email to discuss-leave@lists.opencpi.org
Looks like a lot of the embedded images got stripped out or added as
attachments, which is unfortunate.
If you struggle to read the second part of this, I can try screen grab it
and upload the image somewhere. Or something like that.
On Tue, Jan 30, 2024 at 9:35 PM Dominic Walters waltersdom@googlemail.com
wrote:
Hi,
Apologies for the delayed response to this.
I asked this question to several people who were / are involved with the
creation and maintenance of this worker / component.
These are their responses, which I have slightly edited to fix formatting
and remove names, etc.
I hope the formatting is retained or this might be quite hard to read :D
--- First Response ---
This is explained in the documentation:
However, the term carrier_amplitude may be misleading, carrier_gain would
be better.
In (9) we are looking to define the gain A for some given complex sample -
the gain is relative to the input so we consider the input on a unit
circle, i.e. x and y are in the range -1 to 1.
Substituting in (9) for the point where the term multiplying A is maximal
(x = x_max and y = -x_max):
A ( x_max * cos (theta) – (-x_max) * sin( theta) )
----------------------------------------------------------------- < x_max
2^15
As x_max is 1 and the largest value of cos(theta) + sin(theta) is sqrt(2)
we then get:
A * sqrt(2)
-------------- < 1
2^15
Solving for A:
A * sqrt(2)
-------------- = 1
2^15
A * sqrt(2) = 1 * 2^15 = 2^15
A = 2^15 / sqrt(2) = 23170.475….
A is scaled by 1.64…. and so carrier_amplitude should be set to 14070 for
a gain of 1 through the component.
However, the underlying cordic can over/under-shoot so we recommend using
the value 14,060.
There is (in my opinion) an unnecessary limitation in the C++
implementation which sets an upper bound of the carrier_amplitude value to
14,060 – it is perfectly reasonable to use this component as a gain block –
i.e. setting the value to 28,000 would double the output amplitude relative
to the input.
(if you consider the input to be half scale (x = 0.5, y = 0.5, x_max = 1)
and substitute in (9) you get 28,140).
I did test the RCC implementation and the above holds, I believe the RCC
and HDL implementations are both tested against the same Python based model
– so have no reason to expect the HDL version is any different.
*--- *Second Response ---
I have been doing some thinking on this also and I think I see what Dan is
getting at…but also understand why it is designed as is.
The issue Dan is bringing up is specifically with this bit -> “A is
maximal (x = x_max and y = -x_max)”. If the carrier mixer input is a
“perfect” iq tone, as it is in Dan case, with sin and cos waveforms 90
degrees apart the condition “x = x_max and y = -x_max” never occurs (see
below that there is never a point in time where x is 1 and y is 1 (or -1)).
[image: cid:image003.png@01DA5377.D1D769A0]
Euler’s formula is the easiest way to understand this (I reckon…):
When frequency shifting, Dan wants to realise the below formula, where is
the input signal and is the generated signal.
However, what is currently done is an acknowledgment that the input
waveform might not be a “perfect” since wave and therefore is accounting
for the “x = x_max and y = -x_max)” condition occurring.
So the term is reduced to , since the magnitude of gives 1, which
ensures whatever the input is there is no overflow. To be clear, the is
and (the amplitude of the generated waveform).
In summary, I think how we have it implemented now is correct since it
ensures a messy input waveform never overflows on the output when it is
mixed. But a good compromise to allow for Dan’s “perfect” input waveform
use case is as the first reply says: adding the ability to set the
carrier_amplitude to a value such that an amplitude of 32767 instead of
23170 is achieved for the generated waveform.
I will relay this information onto the ocpi.comp.sdr developers to add to
their backlog.
I hope this was helpful.
Kind Regards,
Dom Walters
On Wed, Jan 24, 2024 at 4:22 PM dwp@md1tech.co.uk wrote:
Hi,
I want to use the carrier_mixer_us in ocpi.comp.sdr.dsp component to
down convert a signal.
Ideally I would want the input wave to have the same amplitude as the
output wave however this does not seem to be possible due to the
carrier_amplitude property having a maximum allowed value of 14,060.
Since the property is scaled by 1.646760258, this brings the amplitude of
the mixer wave to 23170.475 or roughly sqrt(2) * 2^15. I would understand
if the amplitude was limited to 2^15 to prevent overflow but what is the
reason for this sqrt(2) factor?
Before outputting, the result of each multiplication is shifted right by
15 (both I and Q) i.e scaled by 1 / 2^15. Therefore with the maximum mixer
amplitude, the resulting wave’s amplitude will be roughly 1/sqrt(2) that of
the input wave.
It is also quite counterintuitive that the input amplitude of the carrier
wave is being scaled this way. Would it not be possible to provide the true
amplitude to the carrier_amplitude property and have the worker do the
necessary scaling? If not, renaming the property to indicate that it is not
the actual amplitude would be useful.
Thanks,
Dan
discuss mailing list -- discuss@lists.opencpi.org
To unsubscribe send an email to discuss-leave@lists.opencpi.org
Hi Dom,
Thankyou for looking into this and please pass on thanks to the people you had these replies from.
This has cleared things up for me.
I have been looking at the component .rst files for documentation up to now however the online documentation linked is much clearer and the equations and displayed correctly. I will make sure to refer to this in future as well as the .rst files.